Egg-Drop Challenge

Students of Mechanical Engineering Design were divided into teams. Each team was given a raw egg and a package of identical construction materials - such as cardboard, lengths of balsa, duct tape, cord, wire... etc.

The Egg-Drop Challenge was envisaged as an simple event of an egg would be dropped from the second floor balcony of the engineering building thereafter to land upon the first floor in the lobby on the concrete first floor. The teams were given a week to imagine, design and construct some manner of "carrier" such that the egg would survive the fall, would land safely, with its shell unbroken.

One team devised a "glider contraption." The glider stalled; its egg was smashed.
A small "parachute" failed at its task.
Another team built a box of thin, frail slats of balsa. The egg was to ride in the chair. Upon impact with the floor the "chair" would be splintered, the egg saved. They called it a "Frangible Chair." Indeed the chair "franged." It splintered and the egg splashed about the lobby.

Knowing what we know about eggs and concrete, to accomplish this feat seems not even remotely possible. However, an art major had heard of the "Challenge." After the last team's egg was smashed she asked loudly, "Can I try?" Who could say No?

"My Egg-Protector," she explained, "is three pounds of sculpting clay. I softened the clay then formed it like a bird's nest with a thick, clay bottom." She released the egg and clay from the Balcony. It impacted the lobby floor. On their knees, for careful inspection... the egg shell was seen to be intact. Her entry, because it used an "illegal material", was disqualified.

Event Description: The events of the eggs are quite similar. We discuss this in four time-wise stages.

(1) Initial State: Prior to any change each system resides in a permanent state of constrained equilibrium meaning the gravity force and supporting force are equal and opposite. This state, often called the "initial condition" is maintained so long as the student maintains a tight grip. We associate the initial time to be anytime prior to event. Time: t_init = 0.

(2) Catalyst: A system in equilibrium will remain so until "something" sets it "out-of-equilibrium." But once the "something" acts, the system seeks a second state of equilibrium. That "something" is called a catalyst. For a gas-filled room, a spark would be the catalyst. For a system "hanging by a thread" a simple cut would be cataclysmic. The trigger of a pistol acts as a catalyst. With the Egg-Drop scenario, the catalyst is the "release of grip" of the student. The time immediately after trigger-pull is : t = 0+. The catalyst action itself involves very little system energy but promotes much greater system change.

(3) Event Progress: Progress for the eggs is that of falling. This will continue until the system encounters a second set of constraints, i.e., the concrete floor. Time: t = t^*

(4) Final State: The time of the final state is selected depending on what final condition is under study. One choice might be the instant before impact. Or the instant after impact or any time thereafter. The terms, "start-stop", "increment" and "batch process" are used.

The event of interest to us begins upon release of the egg with its kinetic energy, KE_init=0, and its potential energy equal, PE_init = mgH. An instant after impact the is kinetic energy, KE_init=0 and its potential energy equal, PE_init = mgH.the

Δ(KE + PE) = W_1-2

and its potential energy equal, PE_init = mgH.

======= Intro Below ==========

Ideal Bounce

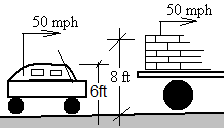A son with his date is driving his father's Mercedes, safely, at 50 miles per hour but maybe a bit close behind a truck loaded with bricks. Placing her hand on his arm, his date says, "Oh Honey, is a brick falling off that truck?"

The sketch shows the scenario.

Is there any chance the brick might bounce over Dad's Mercedes?
♦ This will be a "batch" event that starts the moment the brick falls from the truck and ends at the greatest height it might attain finally.

About Approximation: In general, approximation means the disregard (or set to zero effect) of some aspect of the physical situation being analyzed. Approximation is always used and always simplifies problem analysis. To start, the physical terms and mathematic representations of systems and events, such as mass change, energy change, et al, apply only "on average." To model in finer detail yields better solutions but at the expense of dealing with wilder, unwieldy mathematics. Approximation is expedient but sometimes a necessity.

assuming a "perfect" bounce. For the brick taken as a BODY energy equation is:

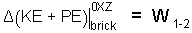
(1)1

For the "bounce event" the second possible elevation will be greatest when there is no work. So we assume "no work." Thus:

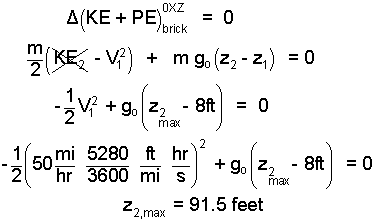
(2)2

Wow! Our calculations predict the brick might bounce upward 90 feet. So there should be no problem for Dad's car... Right?

Our calculations assumed energy of the brick to be conserved. We know that won't happen. However, our calculations are correct - subject to our assumptions.

Although initial calculations require assumptions, their answers are not useless. With assumption our answers become a "bound" for reality. So what can his date say to this Dude with certainty?

Honey, the brick might bounce, but no higher than 91.5 feet!