Geostationary Orbits

Communications rockets routinely place telecasting satellites in Earth orbit such that they maintain a constant position above and relative to Earth. Such orbits, called geostationary, are possible only within the plane of the Earth equator. Rockets place the electronic packages at the proper altitude and with the proper circular velocity. Orbit established, the satellite will remain stationary (relative to Earth) and directly above some point on the equator of earth. This permits Earth-surface communication satellite dishes to be "pointed" in a specific directions to constantly receive satellite telecasted information.

The position of the satellite (above ground in the plane of the equator) can be selected. Physics of Earth motion prescribe the altitude and velocity.

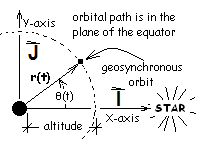
Calculate the altitude of a geo-stationary orbit. The figure (right) depicts a satellite orbiting in the plane of the Earth equator. 0XY coordinates are drawn. The X-axis is locked (at mid-night) to point at a far distant star. The Y-axis is perpendicular to X. This coordinate-pair is assumed inertial. Put otherwise, Earth is assumed to move in a straight line.

The time dependent position of the satellite,P_sat(t), is written as:

(1)

Position of satellite above center of Earth.

The velocity is the derivative of position:

(2)

Velocity of satellite at altitude.

Next multiply Eqn-2 by the satellite mass. Place the factor, dθ(t)/dt to the right. Eqn-3 is the satellite momentum.

(3)

Momentum of the satellite.

Next write Newton's Second Law:

(4) 4

Now enter momentum (Eqn-3) into Eqn-4. Also write the gravity force.

(5)

A longer equation needs more paper.

In the differentiation above, left of equality, keep in mind that dθ(t)/dt is a constant. This angular speed of the satellite is 2πrad/24hr. Differentiate then gather terms.

(6)

Write more compactly, as you go.

(7)

Is this right? Check everything above.

(8) 8

Our answer, 26,261 miles is referenced to the Earth Center. Accounting for the diameter of Earth, changes the above answer to 22,298 miles (above Earth surface).

In Brief Review: Proper, inertial coordinates were established (otherwise Newton's 2nd Law could not be applied). A sketch of the situation was made. The position vector was written using sine and cosine functions with the vector basis locked to Earth. The unit vector I is directed at a distant star (as is J). The Z-axis aligns with the Earth-axis of rotation; that unit vector, K is perpendicular to the plane of the equator. The only calculus needed is that one be able to differentiate the sine and cosine functions.