| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 56 |
1.24 Vector Basis: Circular Motion
Motion of a BODY at constrained by forces to follow a circular path is kinematicly described by the radius of the circle and vectors that depict its position P(t), velocity V(t), and acceleration, A(t).

The graphic (right) shows circular geometry described with positive change of angle, θ(t), and angle rate, d(θ(t))/dt set counter-clockwise, arbitrarily. To Earth-bound coordinates, X, Y (Z-vertical to the page) we assign the vector triad: I, J (K vertical the page). Position of the BODY using these coordinates and basis is written:
| P(t)BODY = r [cosθ(t) I + sinθ(t)J] | (1)
Position of a BODY restrained to a motion in "circular domain" as a function of time. |
In what follows we will not carry the notation "BODY." The derivative of position, Eqn-1, with respect to time yields the velocity of the BODY (V(t)). Next the derivative of that velocity (which is the second derivative of the position) produces a mathematical expression of the acceleration of the BODY ( A (t)). Below, each is written in a "magnitude times unit vector" form where the unit vectors, I and J are fixed in direction. The vectors are:
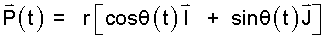 |
(2)Position |
And the derivative of (2),
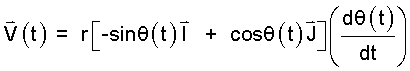 |
(3)Velocity or dP(t)/dt. |
And the derivative of (3),
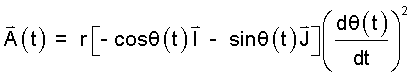 |
(4)
Acceleration: d(dP(t)/dt)dt or dV(t)/dt. |
Problems can be solved with the above set of vectors written just as they are. However a simpler, less writing-intensive vector representation is available. We will use the "truth" of the above set (which you can see) to confirm a simpler representing of P(t), V(t) and A(t)..
Once again, notice the above three vectors are written in magnitude-unit vector form. Compare the "direction" parts (the unit vector parts) of the vectors (2), (3), and (4). Immediately we see the direction of A to be opposite to the direction of P.
Next, using a simple sketch, we see the direction of velocity, V is perpendicular to the direction of P, and it is directed toward increasing angle, θ. Thus we define er(t), and eθ(t).
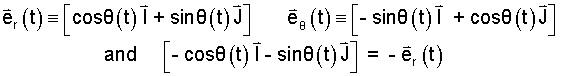

The graphic representation of the new unit vectors with analytic statements of position, velocity and acceleration vectors are shown (right).
| P(t) = r er(t) | (5)
Position: r is constant. |
| V(t) = r(dθ/dt)eθ(t) | (6) dθ/dt is the constant rate of rotation. |
| A(t) = - r (dθ/dt)2 er(t) | (7) Here the rotation rate (dθ/dt) is squared. |
Extension of this idea to apply to non-circular motion, that is for a radius that varies in time, r = r(t), follows easily since the radius is a scalar. The new vector basis described here is:
| er(t), eθ(t) and K, (when needed) | (8)
The vectors apply to motion in plane. |
The vectors discussed here apply for motion of a body "in a plane" about some point, with constant distance from it. These represent a number of physical cases. To extend the motion to include variation of the radius (but still in a plane) would be the next step of study.
1.25 Vector Basis: Circular Motion
Motion of a BODY at constant speed constrained by forces to follow a circular path is kinematically described by the radius of the circle and vectors that depict its position, P(t), velocity, V(t), and acceleration, A(t).