| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 31 |
1.12 Steps to Integrate
Physical laws of mechanics and thermo- dynamics are expressed as first-order ordinary differential equations. Presented below is a simple, time-dependent first order differential equation with its initial condition. We solve the differential equation then we show (in reverse) that the original differential equation is the resuilt of differentation of its solutiion.
Equation with initial condition:
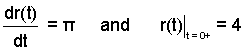
We need to be able to solve the above type equation. All others in thermo and fluids are much the same except for other notations for terms. The steps below are the same ALWAYS."
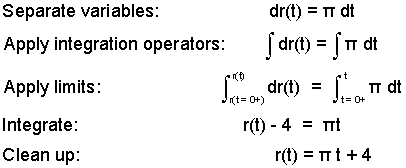
Above we see the differential equation and the steps to obtain its solution subject to the prescribed initial condition.
"Tell me," you might be asked. "Given this solution (the one above) what differential equation belongs to it?
So you go at the solution as below and create the differential equation it belongs to ~ as shown.

1.13 Steps to Integrate
Of calculus, at this level, we need know only the definition and meaning of Newton's derivative. Physical laws for thermodynamics are expressed as first order ordinary differential equations. Presented below is a simple, time-dependent first order differential equation with its initial condition. We solve the differential equation then we show (in reverse) the differential equation that belongs to our solution. This is the differential equation we solved in the first place, of course.
Premise presently unwritted!