Emergency Power Package

A question at Physics Help Forum 
caused me to look into this problem 
presented in Thermo by Moran and Shapiro.

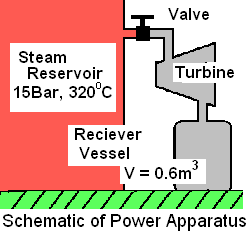
An example in the thermo text by Moran and Shapiro provides the schematic (right) then proceeds to calculate the work that the apparatus might produce when activated. The authors provide the information of the sketch and the final pressure and temperature of the steam; 15 bar and 400°C.

Note:  Moran and Shapiro have selected a peculiar title. Power is energy delivered over a span of time. This apparatus is likely to operate only a short time. However, the authors do not investigate power. Rather, the example calculates the work of the imaginary event. A solution of the example is provided below.

System and Event:   By the scenario schematic it is clear that the event commences when the valve is opened. Steam from the reservoir passes through the valve, then the turbine, headed to the receiver vessel.

A system is chosen to be the interior of the apparatus. The system initially
(t < 0) is empty. The event commences when the valve is opened (t = 0+). The event ends some undetermined time later (t = t _final) when the pressure within equals 15 bar everywhere. We assume the duration of the event (t_final - 0+) to be small; thus there is insufficient time for heat; the event is assumed adiabatic.

Mass Equation:  The mass equation is written with two reductions for the "system/event" indicated. The system has only one place of mass entrance (a) and no places of mass exit (b).

(1)

The mass equation with 
non-relevant terms struck out.

The resulting "reduced" mass equation is shown below left. To proceed to solution the variables of this first order differential equation are separated then the equation is integrated in time between initiation and completion of the event. That is between, t = 0+ and t = t_fin. Shown below right.

(2)Mass equation for one entrance is written. Next, variables are separated and integration with proper limits is applied.

Integration yields below left where the mean value theorem (MVT) is used to integrate the term right-of-equality.

(3)The solution is intuitive. The second mass of the receiver equals the mass that entered. A common notation for increment of mass is "δ".

We have enough information to calculate m_sys,2 = V/v₂. The mass equation informs us, logically, that the second system mass equals the mass that enters.

(4)(4)

Consequences for mass of the apparatus/event are intuitive.

Energy Equation:  Solution of the mass equation is worthwhile since it sets the pattern for the energy equation. Our energy equation reduced by previous considerations is:

(5)The energy equation is reduced as was the mass equation.

The change kinetic and potential energies of the system are assumed small - (c). The kinetic and potential energies of the entering mass are also assumed negligibly small - (e). The "system expansion work" is zero (d) because the system volume is constant. Finally heat is assumed zero because of the expected short time of the event - (f)

(6)This equation is "approximate" subject to approximations made.

Solution procedures are the same for all thermo problems. i) Write an accurate equation that includes all possible terms. ii) Remove other terms that do not apply by assumption relative to the event. iii) Separate variables in the equation then integrate between limits.

(7)Separate variables, apply integration: the limits are (1) to (2).

By methods used before, (7) becomes (8).

(8)We used the MVT, Mean Value Theorem, to evaluate the "work integral."

For equation (8) we have determined the values for the masses involved. Also we have the needed internal energy and enthalpy from property tables for water.

(9)(9)

Applying the known quantities to equation (8) we obtain.

(10)It is wise to avoid algebra until the equation contains only numbers and one unknown.

The habit here is to avoid algebraic manipulation of "terms." The mass equation and energy equation are physical in arrangement. What is "left-of-equality" is physically different from what is "right-of-equality." To "do algebra," as a first step "to get X, alone left-of-equality" screws up the meaning of the equations.

That said, at the end of an analysis that seeks work, W, algebra (applied to numbers) usually has meaning. So we rearrange (10) to yield:

(11)(11)

So the work is negative? Is that sign correct? By logic, for the event of an emergency apparatus, work would transfer from the device to the needful surroundings. This is consistent with our analysis. Our energy equation defines work as being positive when it would cause (in the absence of other effects)an "increase" of system energy. The negative of our numeric answer means energy leaves the system - as we expect.