THERMO Spoken Here! ~ J. Pohl ©

TOC     NEXT    ~   119

Work to Move a Wall

A tank contains a shallow body of water. Its bottom, left wall, and ends are fixed. The right wall can be pushed to the left and will remain vertical should that happen. 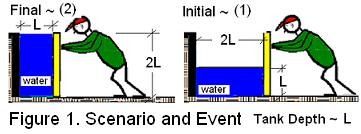Seals prevent all leakage of water. Figure 1. shows the wall in its initial and final positions.

Derive an algebraic expression for the "Least Work" required of the worker to push the wall a distance, L, to the left.

♦ "Least Work" is a highly theoretical consideration. It is the work determined, subject to the assumption that the wall-water-atmosphere system begins in equilibrium. Then, once the event commences, the system proceeds to a final equilibrium state with all intermediate states also being in equilibrium states. Thus the "Least Work Calculation" assumes:
i) the gate will experience no sliding friction, nor will it flex or wobble,
ii) the water surface will rise uniformly, remaining perfectly and always flat and
iii) no noise will propagate through the air. Some call such events "ideal," "quasi-static," "reversible" or "frictionless."

Least Work can be calculated by either of two methods.
(i)  Work/Energy: When all energy changes of an event are known or can be specified for the event, the energy equation Eqn-1, having work as the only unknown, can be solved for work of the event.
(ii) Force/Displacement: When the force-displacement relationship is known, work can be evaluated by integration of its definition, Eqn-2. This method can be tedious (when done correctly).

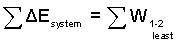(1) Work is calculated "indirectly" as the sum of system energy changes for the event.

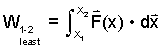(2) Work is calculated "directly" by integration of the force acting through its displacement.

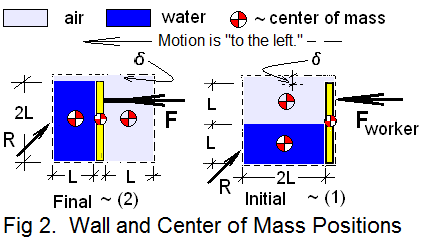
Work/Energy Method:  The wall and water are masses obviously involved with the event. When the wall moves the water moves; these masses are finite. However with movement, so also does the air above the water and to the right of the wall. So we contrive an imaginative system comprised of the wall, water and some of the atmospheric air. The "dashed-boundary" of Figure 2, identifies our system - the masses within that space which has a depth "L" into the page. The space does not move and mass neither enters nor leaves it.

As depicted in Fig-2, leftward movement of the wall (from (1))causes space above the water to be diminished but at the same time creates an equal amount of space right of the wall. As the wall moves, air (within the dashed-line system) from the left passes over the top of the wall and comes to reside in the vacated space right of the wall. For that to happen, our system sketch includes a small "passageway" above the wall, for air to move "left to right." The passage way is very small in height ,δ.

code

Fig-2 shows are centers of mass of the system components (air, water and the wall) in their initial, (1), and final, (2), states. A indicated is the ideal, "least force" applied by the worker to effect the event. A final symbolic force shown, R, represents the reaction of surroundings that maintain equilibrium of the system. This is our system for the Work/Energy Method.

Finally, notice that gravity forces on the wall, water, and air are not part of the system sketch. When the perspective, potential energy, is used it means Earth is considered "part of the system." The attractive gravity force, "Earth on mass" equals the force "mass on Earth." These act in opposite directions; they sum to zero.

Analysis:  The energy types of the wall, water and air are kinetic and potential. The energy equation is:

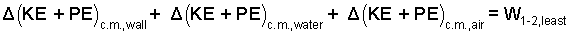(3) The sum of energy changes of three substances equals the work of their event.

Movement of the wall is assumed "very slowly." So slow that kinetic energies, initially, intermediately, and finally are negligibly small, or zero. Eqn-3 becoms Eqn-4.

(4) The sum of potential energy changes of three substances equals the work of their event.

Potential energy change equals mass times local gravity times elevation change.

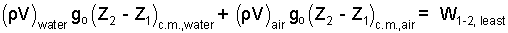(5) Only "water" and "air" experience energy change.

Use Fig-2 to specify volumes and initial and final elevations of centers of mass. Enter these facts carefully while avoiding needless algebra.

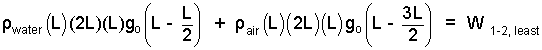(6) For volumes, the dimension into the page is L.

As a final step, apply algebra and rearrange to have "Least Work" left-of-equality.

(7) The contribution of air is very small but need not be ignored.

Force/Displacement Method:   The system is the wall. As it is moved to the left, the the depth of water (ahead, to the left of it) increases. Consequently the force applied by the worker must increase. The depth versus position relation is:

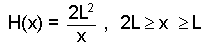(8) Figure 1 goes with Eqn-8. Check the limits!

To write an analytic expression for "F_worker(x)" we apply Newton's 2nd Law to the wall.

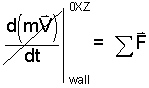
(9) The assumption, "all equilibrium states" means forces sum to zero and paradoxically, the momentum remains constant.

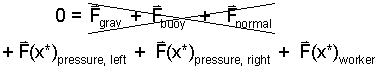
(10) The notation x* means a value of x but not any specific value.

In Eqn-9, the derivative of momentum of the wall is slashed, "/"; meaning, taken to be zero. By assumption, the wall moves so slowly it has near zero velocity.

Eqn-10 lists the forces. The first three are: weight of the wall, the fluid-contact buoyancy forces, and the normal, solid-solid supporting force on the wall from below. These forces act in the vertical and, as a group, sum to zero.

The next three forces (Eqn-10 - second line) act horizontally. These are caused by pressure of fluid-contact of water and air on the wall faces and the force oof the worker. A free-body diagram is needed now. Figure 4 shows the FBD of the wall at an arbitrary position, x*.

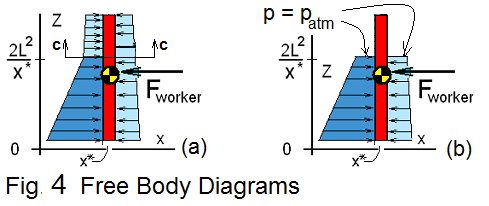
Figure 4(a) shows that the fluid-contact effect of air, acting on both sides, for the section of wall above section c - c is symmetric. Thus the force of air on the left is balanced by the same force of air on the right. Symmetry is a convenient condition. We might also see that p_atm acts on both sides of the wall and might be removed to have an even simpler FBD. Our choice is to use the FBD of Fig-4(b).

The directions of the forces of Eqn-10 are clear. Eqn-11 shows the forces at location, x = x*, written as integrals of pressure force, p(x*,z) over the wall areas of action, 0 ≤ z ≤ 2L²/x*.

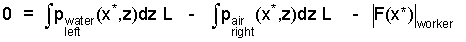(11) Air acts on both sides of the upper, unwetted wall portion.

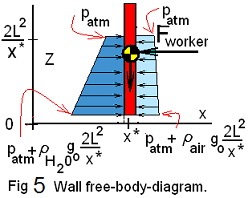Eqn-11 is implicit. To procede we must express the distributions of fluid contact on the wall, p(x*,z). These fluid-contact forces change as the wall moves. The first and second evaluations noted implicitly in Eqn-10. By brief inspection it is apparent that the force contributions of the top and on both sides of the wall are equal and opposite.

The figure shows the pressures at the bottom and the top of the acting fluids. An equation of pressure with vertical value of "z" is:

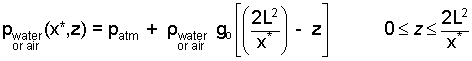
(12) Presure distribution at the inspecific location, x*.

The next step is to insert the expressions (12) into Eqn-11 8. Using it once with water as the fluid (left side of the wall) and again for air as the fluid (right side).

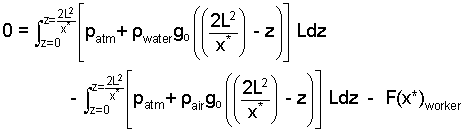
(13)C240_e13

Below the integrations have been performed but limits have not been applied.

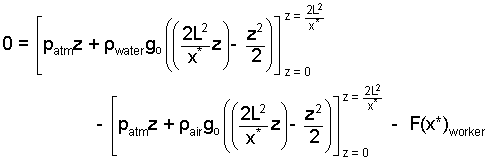
(14) Take care with these manipulations.

Do the step, "apply limits," carefully.

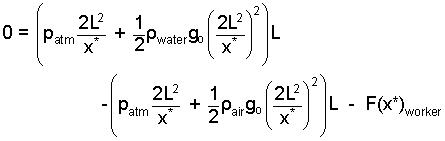
(15) The fluid-contact forces vary with location, "x." This equa- tion defines the force at the inspecific location, x*.

Integrations are completed and the equation is "tidied-up". The next equation has only the force required of the worker as unknown. The equation applies at wall location x* but since this is an arbitrary location, the equation applies at all values of x.

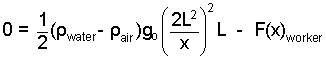
(16) Maybe I should have integrated using, "-dx." What do you think?

Terms of the above equation are forces. The work of a movement of the forces is determined by scalar multiplication of the equation by the displacement, dx(-I) (the wall displacement is in the direction, negative I.

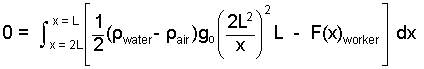
(17)Equation (16) multiplied by dx(-I) then integrated from x1 = 2L to x2 = L.

The integration is perfunctory. With a step or two we arrive below.

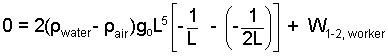
(18) One step at a time!

So, we arrive at an answer.

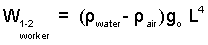
(19) Same answer as the Work/Energy Method.

Thankfully, the same answer as with the "Work/Energy" method was obtained.

Work to Move a Wall

A tank contains a shallow body of water. Its bottom, left wall, and ends are fixed. The right wall can be pushed to the left and will remain vertical should that happen. Seals prevent all leakage of water. Figure 1. shows the wall in its initial and final positions. Derive an algebraic expression for the "Least Work" required of the worker to push the wall a distance, L, to the left.

Premise presently unwritted!