| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 114 |
Buoy Lift I
 The sketch depicts a buoy floating in the sea. A cable is lowered from a dock and attached to the buoy (State 1). The event is that by the cable, the buoy is hauled to State 2.
The sketch depicts a buoy floating in the sea. A cable is lowered from a dock and attached to the buoy (State 1). The event is that by the cable, the buoy is hauled to State 2.
Calculate the least work of the cable for this event.
♦ We take the buoy, modeled as an extended body, as system. The buoy center of mass (c.m.) is closer to its bottom than its top. The event occurs between the times, t1, (which equals the time of initiation, t = 0+) and t2, the time the second conditions are attained. The sketch shows the second state conditions of the buoy. The energy equation increment form is:

| (1) 1 |
Next write the kinetic and potential energy changes of the buoy explicitly:

| (2) 2 |
Information from the sketch can now be entered. Notice that the surface of the water is taken as the datum (zero) for potential energy and elevations are determined relative to the center of mass of the buoy.

| (3) 3 |
We expect the units of "Newton-meter," throughout.
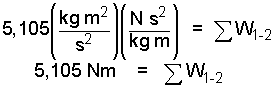
| (4) 4 |
Our reduced energy equation makes it clear that this work calculation is indirect. That is, work is determined as being a consequence of calculated system energy change rather than a force-displacement integration. We have determined ΣW but we seek the work that occurs at the cross-sectional part of the boundary that cuts through the cable. To proceed we peruse the system boundary in search of forces other than cable tension that have been displaced.

i) Atmospheric pressure acts across the top of the buoy. That pressure times its circular area, patmA, is a force acting downward.
ii) Pressure-forces acting about the cylindrical area of the buoy side are displaced but perpendicular to their lines of action. Hence there is no work.
iii) The pressure force of the water acting over the bottom of the buoy equals:
(patm + ρgoz)A or (patmA + ρgoAz)
where z is the depth of the bottom as it is lifted. This force acts upward.
It is always worthwhile to draw a force-displacement sketch. It is logical to have z as the ordinate.
 The displacement of the bottom of the buoy begins at z = -2.0 m where the force is:
The displacement of the bottom of the buoy begins at z = -2.0 m where the force is:
F(z = - 2 m) = - ρsea watergo A(- 2.0m).
With upward displacement the force diminishes linearly to become zero when the buoy bottom attains the surface, z = 0.0 m. The correct equation for the force on the bottom as a function of "z" is:
F(z) = - ρsea watergo Abottomz, for -2m ≤ z ≤ 0m .
Returning to the energy equation (4) we write the work as being part that of the cable and part being that of the sea water.

| (5) 5 |
Next we write the work of the sea water as the integral of its force as it varies over its displacement. These details are shown below.

| (6) 6 |
As with all calculations at this level, the answer is only a bound. Since friction was assumed zero, 4,100 Joules is the theoretical minimum work required via the cable.
Buoy Lift I

The sketch depicts a buoy floating in the sea. A cable is lowered from a dock and attached to the buoy (1). The event is that by the cable, the buoy is hauled to a second state, (2).
Calculate the least work required of the cable that lifts the buoy.
Premise presently unwritted!