Galileo's Experiments

Galileo, who died shortly before Newton was born, attempted to determine the free fall acceleration of a BODY caused by Earth's gravity. Having encountered the difficulty in measuring characteristic of vertical fall of a BODY, Galileo decided to diminish the effect, to slow the event of free fall so it could be measured.

To do this he constructed a very smooth and rigid, inclined plane. He dusted the plane with powder and used a steel cube as the BODY. With many many experiments Galileo...

He measured time versus distance of travel to calculate Earth's gravity, g_o. Suppose on one test (geometry as shown) Galileo used powder on the ramp and a small cube of steel. The time of the slide he measured at 2.4 seconds. Assume the cube to slide down the plane without friction.

What Value of g_o did his experiment predict?
♦ In his life, he had attempted to determine μM_E by "slowing" the effect of gravity on free-fall of a body. He studied the motion of bodies moving down inclined planes. Specifically, he measured time versus distance-of-travel and used that information to calculate Earth's gravity, g_0,E.

For one test (geometry as shown) he used a small, highly-polished cube of steel. He observed the cube to slide down the incline a distance of 216 centimeters in 2 seconds. What value of g_0,E did Galileo's determine?
♦ This discussion is a bit advanced (in the direction of learning toward understanding). We will use "proper math" (vectors) with a stratagem to deal with "an inclined plane."

This will be a special coordinate system (0'X'Z') with the X'-axis parallel with the plane (and increasing "up the plane"). The unit vectors are then I' and K'. The free-body diagram shows this information. The momentum equation and its forces are written below:

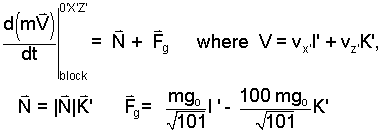
(1)

We proceed carefully by writing the normal and gravity force vectors in component form (above), then placing them in the momentum equation (second law) below. Motion involves the "up or down hill" the I' component. Hence we scalar multiply by the vector direction - I'. Recall that I' • I' = 1 and I' • K' = 0.

(2)

So here we are again. The above first order differential equation tells us the change of momentum of the block is a constant. Initially the velocity of the block is zero and we place the beginning of the coordinate space (0X'Z') to be the beginning position. The relevant space for the slide is 0X' and the - on the term right of equality means the block moves leftward, down the plane. Though Galileo had no calculus, he knew the velocity and position of the block to be.

(3)

Applying the numbers of his test into the equation (above right) we obtain:

(4)

The value we use is 9.81 m/s² So Galileo's answer was reasonably close.