| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 40 |
1.18 Differentiation: Time Dependent Integral
A simple proof needs a “dummy variable” approach.Also needed is the “Mean Value Theorem."
Time is relevent to every physical analysis. The basic characteristics of of motion are position, velocity and acceleration. It is inportant, given any of the three, to integrate ofr differentialt (as the case might be) to obtain teither of the other two. Of course the relations are sound. But the calculus can get a little sticky. This partial review of basic, definitional, calculus.
Scenario: Suppose at a time we designate as t = 0+, a BODY is located at the position, P0+. Suppose further that at t = 0+ and for times thereafter the velocity of the BODY is know by the implicit function, V(t). By this information we can write the position of the BODY as:
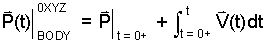 |
(1) 1 |
What is described mathematically is the position in space of a our system modeled as a BODY. Position (in the equation)is superscripted "0XYZ" to convey that a cartesian space has been defined (origin, coordinate axes and a vector basis) and subscripted "BODY" to designate the system. Position is a vector; vectors are written with and "over-bar."
Determine the derivative of P(t).
♦ Differentiation, a mathematical process, has precise steps. The first, symbolic step is to apply the differentiation operator, "d/dt" to the entire equation.
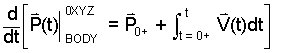 |
(2) 2 |
The derivative of an equation equals the equation with the derivative taken of each of its terms (Eqn 3). The derivative of the position, P, of a BODY is defined by Newton to be its velocity, V(t). Also the derivative of the constant initial position, P0 equals zero (Eqn 4).
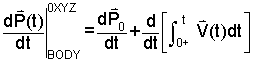 |
(3) 3 |
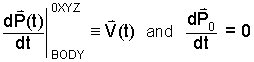 |
(4) 4 |
Substituting items (Eqn 4) into (Eqn 3) we obtain:
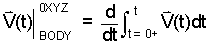 |
(5) 5 |
The above is correct. To prove that is so, we continue manuipulation of the right side of the equation until it is transformed to V(t).
For clarity, we momentarily cast the integral (Eqn 5) as a nested term. Define V(t) as (Eqn 6) with Ψ(t) defoned as (Eqn 7).
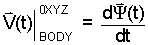 |
(6) 6 |
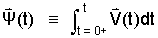 |
(7) 7 |
On the right side of (Eqn 6) change derivative notation from "d/dt" to the expression, "the limit of the difference quotient of Ψ(t)."
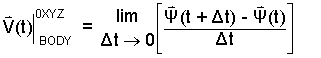 |
(8) 8 |
We see immediately that Ψ(t) is known: (Eqn 7). Then using the definition (Eqn 7) we promptly construct Ψ(t + Δt) and insert these two into (Eqn 8):
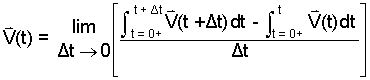 |
(9) 9 |
Upon inspecting (Eqn 9), those who know calculus will know the statement is wrong. Why? This writing walked us into this mistake as an easier way of explaining its error.
Dummy Variable:
To correct the error, we return to (Eqn 1). The integral of the equation is written, as is common, having the variable "t" in its upper limit, as the dependent variable of the integrand and as part of the differential. These "t's" are not the same. Some call the "t's" of the expression "V(t)dt", dummy variables. Their do bnot appear in the integrated result; their purpose it to effect the integration only.
Error would have been avoided had (Eqn 1) been written diferently, that is as (Eqn 1').
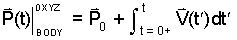 |
(1') 1' |
We can skip to (Eqn 9) above. Our path is to use a correct derivative of the above. We write the difference quotient as (Eqn 9'):
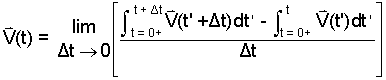 |
(9') 9' |
By properety of integrals, the above equals:
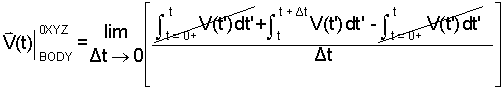 |
(10) 10 |
Mean Value Theorem:
Regarding the remaining integral, we apply the Mean Value Theorem of Calculus. By the theorem, the integral becomes:
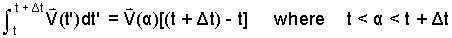 |
(11) 11 |
Substituting the theorem result into (Eqn 10) we have:
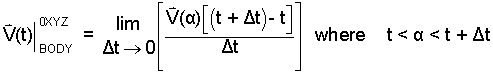 |
(12) 12 |
Notice within the limit t's sum to and then "Δt/Δt =1." Also for the limit, notice that α is squeezed between t and t + Δ. So as Δt vanishes, α becomes t.
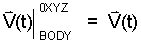 |
(13) 13 |
1.19 Differentiation: Time Dependent Integral
This simple proof leads to the idea “dummy variable”. Also the “Mean Value Theorem is used." This is important calculus for physics.
Time is relevent to every physical analysis. The basic characteristics of of motion are position, velocity and acceleration. It is inportant, given any of the three, to integrate ofr differentialt (as the case might be) to obtain teither of the other two. Of course the relations are sound. But the calculus can get a little sticky. This partial review of basic, definitional, calculus.
Premise presently unwritted!