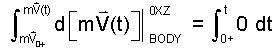| THERMO Spoken Here! ~ J. Pohl © | TOC NEXT ~ 21 |
1.10 Uniform Motion: BODY
Two characteristics of a BODY (existing in a defined 0XYZ space) are its position, P, and its velocity, V. Two properties of the BODY are its mass, m, and its mass-velocity product, its momentum, mV. Newton used calculus to develop a single description of motion of a BODY in space. Today his First and Second Law are aptly expressed by the following, single, differential equation:
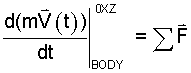 |
(1)
Of possible motions, uniform motion, for which momentum of the BODY is constant, is least complex. |
The equation is an implicit description, it specifies, when the sum of forces is known, all manners of motion of a BODY. Of those motions, uniform motion, for which momentum of the BODY is constant, is the least complex. For motion with constant momentum, the above equation becomes two ideas which are expressed mathematically as:
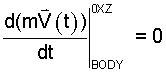 |
(2)2 | 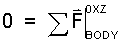 |
(3)3 |
Physically, since they share equivalence to zero, the equations say the same thing. Equation (2) states "momentum of the BODY is unchanged as time proceeds." Equation (3) states the supporting fact; "the sum of forces acting on the BODY equals zero." Forces are constructs, characterizations of whatever might change the momentum of the BODY as time proceeds.
To study further we must follow the two branches of logic that share this zero. We are at the beginning, very simplest level of mathematical physics. Let us make equation (2) specific to the case it defines then solve that differential equation.
Constant Momentum Motion (with zero initial velocity) In mathematics when someone says, "that's trivial," they mean that the solution is known, patently obvious and a waste of time to prove. Nonetheless below is solved what might be called the "trivial case," the easiest application of Newton's Laws of Motion. The system is a body with constant momentum and a zero initial velocity. Newton described the case with the words:
"A body at rest remains at rest provided (and as long as)
the sum of acting on it equal zero.
Below left is shown a schematic of the scenario (with notations). This body moves in an 0XZ space (for convenience we omit the Y coordinate). To its right is the governing differential equation.
 Scenario Schematic: Body at Rest  System Schematic: Body at Rest |
Momentum Equation: |
(4)4 |
Superscript: Space Domain: 0XZ | (5)5 |
Subscript: System as a BODY |
(6)6 |
Initial Conditions: |
(7)7 |
Time Domain; |
(8)8 |
Mathematically we have a first order differential equation of the vector property, momentum, of a BODY. Momentum is the differential equation's (time-) dependent variable and time is its independent variable. The domain of time starts at the initial instant of observation (t = 0+) and continues for all times thereafter. (Often the initial time of observation and the commencement of the event are the same time.) The differential equation states that the time derivative of momentum of the body is always equal zero. The initial condition (at t = 0+) is that the velocity of the BODY equals zero. Note: we write body as BODY to emphasize the mental process of identification of the system. The Solution means to determine Vbody(t) for all times t ≥ 0+.
The mathematical task is to integrate the differential equation. This procedure is said to be "classical" which means "at the very basis of mathematics." The first order differential equation is very common. You will see this same procedure executed again and again in your studies. The steps have been taken so often - they even have names!
Separate the Variables: As written, the left side of the differential equation has two variables. The differential of momentum, d[mV(t)] is the dependent variable, time, t, is the independent variable. Upon multiplication of this simple equation by dt the variables become separated to yield:
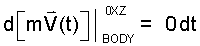 |
(9) These steps are the same, again and again... evermore! |
Integrate the Equation: First apply integration symbols to both sides of the separated equation:
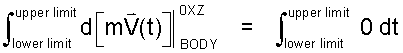 |
(10)
Integration is a linear operator. Its limits are conditions of the BODY as specific times (either known or not known). |
Next, apply limits of integration: To decide limits a good approach is to search among all limits (lower or upper) to find the easiest. Deal with that term first. Here, the "right-side" integral, needing limits in time, is the easier. The event initiates at a definite starting time; the right side lower limit is t = 0+. The upper limit is either an "ending time" or as in this case just "t" meaning any later time. The upper limit is t = t.
Next match conditions of the left-side limits with the already stated, right-side limits. By its upper limit, (t), the right side integration is indefinite; so the left side upper limit is the indefinite quantity, mV. For the lower limit the body momentum, mV0+, (corresponding to time, t = 0+), is zero because the velocity is zero.
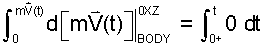
| (11)These integrations with variables as upper limits. are called indefinite integrations." |
Perform the integration... often symbolic:
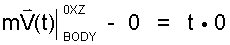
| (12)12 |
INTERPRET RESULTS: The conclusion of our mathematics states:
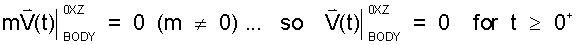
| (13)13 |
The above result states the velocity of the body was zero at t = 0+ and remained zero for all times thereafter. We can take this a step further.
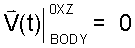 |
(14)14 | 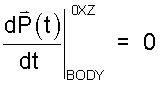 |
(15)15 |
The above first order differential equation requires an initial condition of position to be solved. Obviously the body was somewhere at t = 0+. That place is P(t = 0+). So we repeat the process:
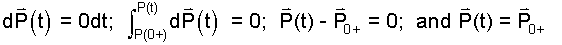
| (16)16 |
This last statement says for all times (including t = 0+) the position of the body is "where it was."
This first solution of Newton's differential equation is trivial in that the answer was known before we started. Nonetheless we solved its first order differential equation. Behaviors of very many physical systems can be expressed mathematically as first order differential equations. Solution steps are classical. So return... reread and confirm that these ideas of space, time frame, initial condition and such are correct. Commit this solution to memory; be able to reproduce it on a bar napkin to impress your date!
Constant Momentum, Non-zero Velocity Motion The next classical solution in this vein is that of a body with constant momentum but non-zero initial velocity. Space and all are defined as before. The differential equation is:
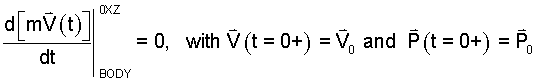
| (17)17 |
Can you solve the above differential equation? Give it a try! The solution is:
Pbody(t) = Pbody,0+ + Vbody,0+ t for all times, t > 0+
It is likely that you've seen this solution in physics but different. To obtain the high school physics form, first rearrange the solution to have the form, P(t) - P0+ = V0+t. Next ignore the obvious idea "where it started" and set P0+ to zero, to have: P(t) = V0+t. Next to avoid vectors change P(t) to S and V0+ to V, both scalars. That is pretty much the way the meaning and diversity of Newton's understanding of uniform is smoked and canned for use in high school physics: S = Vt. Our next example, Yacht and Sea Buoy, illustrates (at a beginning level) uniform motion in which two-dimensional-relative motion is considered.
• Constant Momentum, Non-Zero Velocity Motion Steps of the integration: Newton's First Law of Motion applies to bodies with constant momentum. His differential equation states that momentum (in 0XZ-space) is constant as long as the sum of forces equals zero ( ΣF = 0):
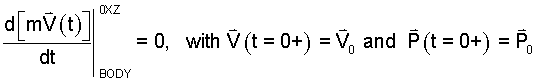
| (18) 18 |
Newton's equation applies for times during which the body is observed. Specific epochs begin at the time, t = 0+, the instant observation commences. The above mathematical statement is inspecific; by itself it has no solution. To obtain a solution an "initial condition," the momentum of the body at the beginning (at t = 0+), is needed. Two cases for constant momentum of the mass are zero velocity and constant, non-zero velocity. The zero-velocity case was solved above. The solution for the second case proceeds as follows.

| (19) 19 |
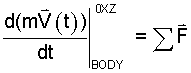
1.11 Uniform Motion
Two characteristics of a BODY (in an 0XZ space) are its position, P, and its velocity, V. Two properties of the BODY are its mass, m, and its mass-velocity product, its momentum, mV. Newton used calculus to develop a single description of motion of a BODY in space. Today his First and Second Law are aptly expressed by a single differential equation.
Premise presently unwritted!